While the developer documentation on $sets and the +in core is comprehensive, it is organized alphabetically which can make it difficult to see what's going on with set relations. This article will describe set identities and relations↗ through the Hoon standard library.
A $set is a tree with a particular internal order based on the hash of the value. This tends to balance the values and make lookup and access more efficient over large sets.
Set Creation & Membership
Define a Set
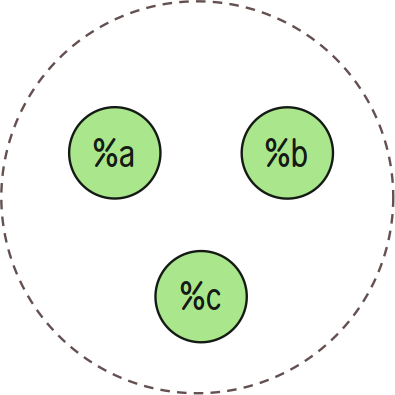
++silt produces a $set from a $list.
> `(set @tas)`(silt `(list @tas)`~[%a %b %c %a]){%b %a %c}
Add Members
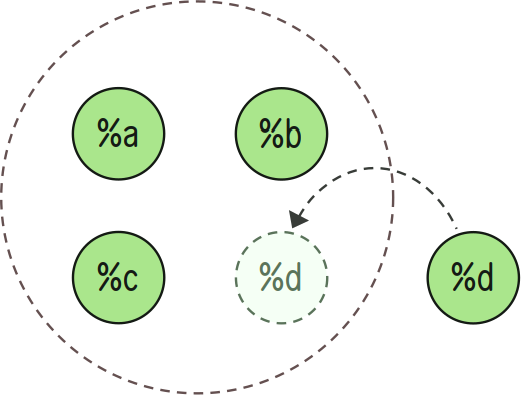
++put:in adds an element x to a set A.
> =/ a `(set @tas)`(silt `(list @tas)`~[%a %b %c])`(set @tas)`(~(put in a) %d){%b %d %a %c}
++gas:in adds each element x, y, z of a list to a set A.
> =/ a `(set @tas)`(silt `(list @tas)`~[%a %b %c])=/ b `(list @tas)`~[%d %e %f]`(set @tas)`(~(gas in a) b){%e %b %d %f %a %c}
Remove Members
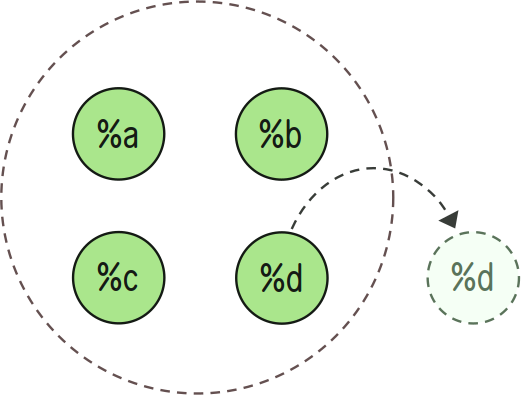
++del:in removes an element x from a set A.
> =/ a `(set @tas)`(silt `(list @tas)`~[%a %b %c %d])`(set @tas)`(~(del in a) %d){%b %a %c}
Membership
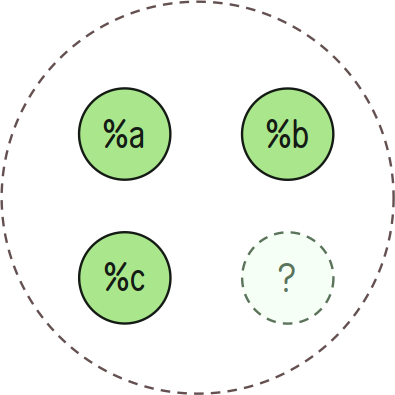
++has:in checks if an element x is in a set A.
> =/ a `(set @tas)`(silt `(list @tas)`~[%a %b %c])(~(has in a) %a)%.y> =/ a `(set @tas)`(silt `(list @tas)`~[%a %b %c])(~(has in a) %d)%.n
Size
++wyt:in produces the number of elements in A as an atom (width).
> =/ a `(set @tas)`(silt `(list @tas)`~[%a %b %c])~(wyt in a)3
Export as List
++tap:in produces the elements of set A as a $list. The order is the same as a depth-first search of the $set's representation as a $tree, reversed.
> =/ a `(set @tas)`(silt `(list @tas)`~[%a %b %c])~(tap in a)~[%c %a %b]> =/ a `(set @tas)`(silt `(list @tas)`~[%a %b %c])=/ b `(list @tas)`~[%d %e %f]~(tap in `(set @tas)`(~(gas in a) b))~[%c %a %f %d %b %e]
Set Relations
First we consider the elementary operations between two sets.
Union (A ∪ B)
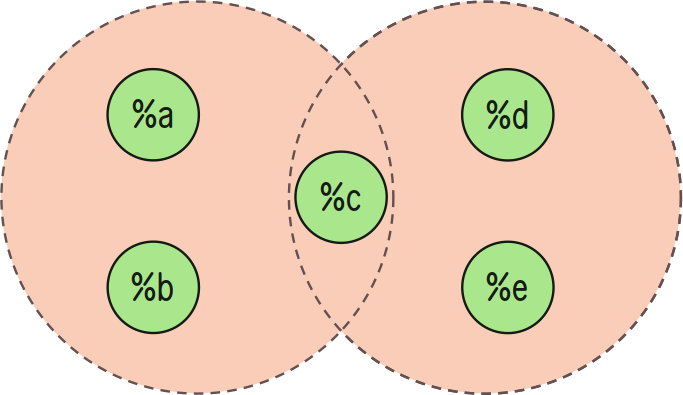
++uni:in produces a set containing all values from A or B. The types of A and B must match.
> =/ a `(set @tas)`(silt `(list @tas)`~[%a %b %c])=/ b `(set @tas)`(silt `(list @tas)`~[%c %d %e])`(set @tas)`(~(uni in a) b){%e %b %d %a %c}
Intersection (A ∩ B)
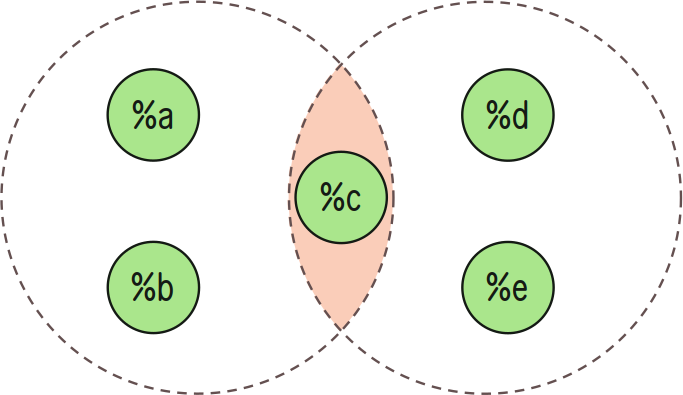
++int:in produces a set containing all values from A and B. The types of A and B must match.
> =/ a `(set @tas)`(silt `(list @tas)`~[%a %b %c])=/ b `(set @tas)`(silt `(list @tas)`~[%c %d %e])`(set @tas)`(~(int in a) b){%c}
If two sets are disjoint, then their intersection is ∅.
> =/ a `(set @tas)`(silt `(list @tas)`~[%a %b %c])=/ b `(set @tas)`(silt `(list @tas)`~[%d %e %f])`(set @tas)`(~(int in a) b){}
Complement (Aꟲ)
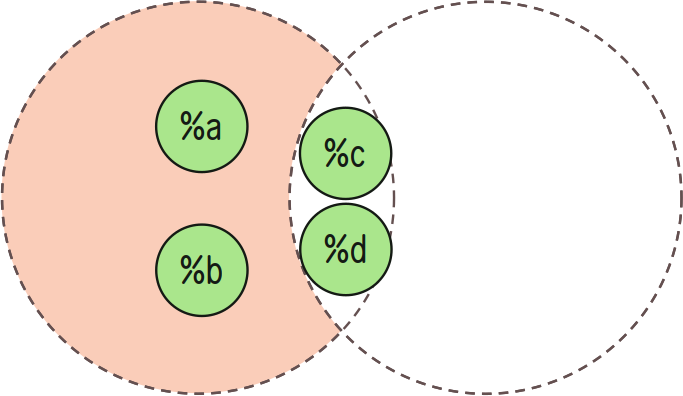
The complement of a set A, Aꟲ, may be found using ++dif (difference).
For instance, if X = {a, b, c, d} and A = {c, d}, then Aꟲ = {a, b}.
> =/ x `(set @tas)`(silt `(list @tas)`~[%a %b %c %d])=/ a `(set @tas)`(silt `(list @tas)`~[%c %d])`(set @tas)`(~(dif in x) a){%b %a}
Symmetric Difference (A Δ B)
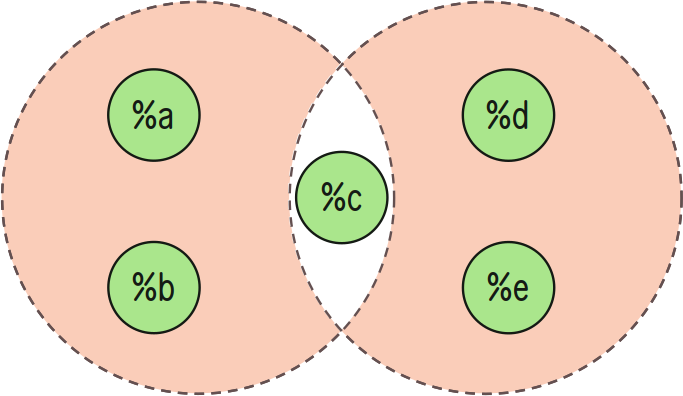
The symmetric difference of two sets A and B consists of those elements in exactly one of the sets. Use ++uni:in with ++dif:in to identify this set.
For instance, if A = {a, b, c} and B = {c, d, e}, then A Δ B = {a, b, d, e}.
=/ a `(set @tas)`(silt `(list @tas)`~[%a %b %c])=/ b `(set @tas)`(silt `(list @tas)`~[%c %d %e])=/ lhs (~(dif in a) b)=/ rhs (~(dif in b) a)`(set @tas)`(~(uni in lhs) rhs)
Set Operations
Logical AND (∧)
++all:in computes the logical AND on every element in set A against a logical function f, producing a flag.
> =/ a `(set @tas)`(silt `(list @tas)`~[%a %b %c])(~(all in a) (curr gth 32))%.y
Logical OR (∨)
++any:in computes the logical OR on every element in set A against a logical function f, producing a flag.
> =/ a `(set @tas)`(silt `(list @tas)`~[%a %b %c])(~(any in a) (curr gth 32))%.y
Operate with Function
++run:in applies a function f to every member of set A.
> =/ a `(set @tas)`(silt `(list @tas)`~[%a %b %c])(~(run in a) @ud){98 97 99}
Accumulate with Function
++rep:in applies a binary function f to every member of set A and accumulates the result.
=/ a `(set @ud)`(silt `(list @ud)`~[1 2 3 4 5])(~(rep in a) mul)b=120
While there are a few other set functions in +in, they are largely concerned with internal operations such as consistency checking.